पुरा कवीनां गणनाप्रसङ्गे कनिष्ठिकाधिष्ठितकालिदासः ।
अद्यापि तत्तुल्यकवेः अभावात् अनामिका सार्थवती बभूव ।
अर्थ : पूर्वी एकदा कवींची मोजणी चालली होती, तेव्हा करंगळीवर कालिदास आरूढ झाला. पण त्याच्या तोडीचा दुसरा कोणी कवी अद्याप न मिळाल्याने करंगळीच्या शेजारचे बोट ज्याला ’अनामिका’ म्हणतात, त्याचे अनामिका हे नाव सार्थ झाले.
हा एक सुंदर श्लोक आहे पण ह्या ठिकाणी तो उद्धृत करण्याचे कारण मात्र त्यातील सौंदर्य हे नाही! त्याचे कारण वेगळेच आहे. करंगळीवर कालिदास आरूढ झाला यावरून काय लक्षात येते? तर गणना करण्यासाठी तेव्हाही हाताची बोटेच वापरत असत. आजही आपण तेच करतो. इतकेच नव्हे तर आज जगभर प्रचलित असणाऱ्या अंकांच्या दशमान पद्धतीचा उगम ह्या दहा बोटांतूनच झाला आहे. digit ह्या इंग्रजी शब्दाचा पहिला अर्थ ’हाताचे बोट’ असा आहे. परंतु अंक मोजण्यासाठी बोटे वापरली जायला लागल्यामुळे अंकांसाठीही digit हाच शब्द वापरायला सुरुवात झाली.
आपल्याला माहीत आहे की दशमान पद्धतीमध्ये ०,१,२,३,४,५,६,७,८,९ ही दहा चिन्हे वापरली जातात. ९ पेक्षा मोठी संख्या लिहिण्यासाठी ह्या दहा चिन्हांपैकीच काही किंवा सर्व चिन्हे वापरली जातात. ह्यामध्ये अंकाची स्थानीय किंमत ही संकल्पना वापरली गेली आहे. दशमान पद्धतीत १० हा अंक मूलांक असतो. संख्येतील अंकाच्या स्थानानुसार त्याची किंमत ठरते. म्हणजे ६७१४ ह्या संख्येतील ७ ह्या अंकाचे स्थान उजवीकडून तिसरे आहे. म्हणून त्याची किंमत ७*१०**(३-१) = ७०० इतकी आहे. प्रत्येक स्थानाची किंमत १० च्या घातामध्ये असते.
दशमान पद्धतीबद्दल आणखी माहिती मिळवण्याआधी, पूर्वी ज्या अंकपद्धती अस्तित्वात होत्या त्यांच्यापैकी काहींच्याबद्दल जाणून घेणे रंजक ठरेल. इतर पद्धतीपैकी रोमन आकडे - I, II, III, IV, V, VI, ..... X, ...L(50), C(100), D(500), M(1000) हे आपल्या परिचयाचे आहेत. ही पद्धती मूलांक आणि स्थानीय किंमत ह्या संकल्पनांवर आधारित नाही. त्यामुळे ह्यात संख्या लिहिणे आटोपशीर होत नाही. ह्या कारणाने ती फारशी प्रचलित झाली नाही. परंतु अजूनही कुठे कुठे घड्याळातील आकडे, क्रमदर्शक आकडे ( first, second, third... ,) लिहिण्यासाठी, किंवा एखाद्या पुस्तकात प्रस्तावना, लेखकाचे मनोगत इत्यादींना पृष्ठक्रमांक देताना हे आकडे वापरतात.
मायन( mayan) संस्कृतीबद्दल आपल्यापैकी काहींनी वाचले असेल. दक्षिण अमेरिकेत उदयाला आलेली ही एक प्रगत संस्कृती होती. त्यांच्या अंकपद्धतीचा उगम चौथ्या शतकात झाला असावा असा अंदाज आहे. ही अंकपद्धती दशमान पद्धतीशी थोडीफार मिळतीजुळती होती. मात्र दशमान पद्धतीत १० हा मूलांक असतो तर मायन पद्धतीत २० हा मूलांक होता, चिन्हे मात्र २० नव्हती. ती होती फक्त तीन! पुढील तक्त्यामध्ये दशमान पद्धतीतील ० ते ९ हे अंक मायन लोकांनी कसे लिहिले असते ते दाखविले आहे. १ साठी ठिपका, ५ साठी आडवी रेघ हीच मुख्य चिन्हे इथे आहेत. (तारायंत्राशी संबंधित मोर्स कोडमध्येही डॉट/डॅश असते. म्हणजे माणसाला स्वाभाविकपणे सुचणारी ही चिन्हे आहेत की काय?!)

तक्ता २ मध्ये एक मोठी दशमान संख्या मायन पद्धतीत कशी लिहावी लागेल ते दाखवले आहे. त्यासाठी तिचे प्रथम दशमानातून मायन मध्ये रूपांतर करावे लागेल. द्विमानात रूपांतर करताना जसे आपण २ ने भागत जातो व प्रत्येक वेळी उरणारी बाकी हा रूपांतरित संख्येतील एक एक अंक असतो. तसेच इथे करायचे, फक्त भागायचे २० ने.

शून्य हा अंक त्यांच्यातही होता पण ही गोष्ट त्यांच्यापुरतीच मर्यादित राहिली. बाहेरच्या जगात पोहोचली नाही. मात्र भारतीयांनी आणलेली शून्याची संकल्पना युरोपापर्यंत पसरली. त्यामुळेच शून्य हे भारतीयांनी जगाला दिलेले आहे असे म्हणतात ते योग्यच आहे.
इजिप्शियन लोकांनी पूर्वी गणितात बरीच प्रगती केली होती, त्यामुळे त्यांची अंकपद्धती कशी होती हे जाणून घेण्याची उत्सुकता सर्वांच्याच मनात असेल. त्यांच्या अंकपद्धतीबद्दल माहिती तेथील शिलालेख, भग्नावशेष, मातीच्या भांड्यांवरील चित्रे इत्यादीवरून मिळते. इजिप्शियन लोकांनी निसर्गातील गोष्टी -पाने, फुले, पशुपक्षी इत्यादींचा वापर करून अंकांसाठी चिन्हे बनवली. त्यासाठी पुढील तक्ता पाहा.

त्यात एकासाठी उभी रेघ दिसत आहे. हे बहुतेक सर्वच पद्धतींमध्ये दिसून येते. पुढे घोड्याचा नाल, दोरीचे वेटोळे, फूल, हाताचे बोट दिसत आहे. त्यापुढील चिन्हे ही टॅडपोल व आश्चर्यचकित झालेला माणूस अशी आहेत असे म्हणतात. ते काहीही असो, पण इजिप्शियन लोकांनी १०च्या घातांसाठी चिन्हे ठरवली हे नक्की. मग २,३,४.. साठी दोन, तीन, चार .. अशा उभ्या रेघा वापरत असत तर २०, ३०, ४० साठी दोन, तीन, चार नाल वापरावे लागत. १७, २५, ४३ अशा मधल्याअधल्या संख्यांसाठी एकाहून अधिक चिन्हे वापरत. उदा:

ग्रीकांकडे तर पायथागोरस, आर्किमिडिज असे एकाहून एक महान गणितज्ञ होऊन गेले, तेही इसवीसनपूर्व कालात! त्यावेळी ग्रीकांनी कोणती अंकपद्धती वापरली असेल? तर त्यांनी त्यांची वर्णमालाच त्यासाठी वापरली. हे साधारण ख्रिस्तपूर्व ४५०च्या आसपास झाले. पण त्यापूर्वी काही काळ ते त्या वेळी अस्तित्वात असलेल्या इतर अंकपद्धतींशी मिळतीजुळती अंकपद्धती वापरत. त्याला ऍटिक पद्धती म्हणत. ती फारशी सोयीस्कर नसल्याने तेवढी टिकली नाही. त्यापद्धतीबद्दलची माहिती पुढील तक्त्यात मिळेल.

वर्णमालेवर आधारित अंकपद्धतीसाठी पुढील तक्ता पाहा.
अशा रीतीने ते ९९९ पर्यंत संख्या लिहू शकत असत. त्याहून मोठ्या संख्या पुढीलप्रमाणे लिहिल्या जात. चिन्हाच्यापूर्वी स्वल्पविराम लिहिला असता त्या चिन्हाची किंमत १००० पटीने वाढेल असे त्यांनी ठरविले. असे केल्याने त्यांना १०,००० पर्यंत संख्या लिहिता येऊ लागल्या. त्यापुढील संख्यांसाठी त्यांनी आणखी एक युक्ती केली. M हे अक्षर १०,००० साठी ठरवले आणि १०,००० च्या पटीतल्या संख्या M च्या वर लिहायच्या असा नियम केला.
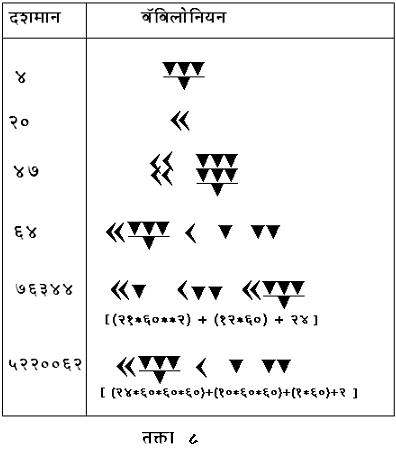
बॅबिलोनियन संस्कृतीबद्दल आपण इतिहासात वाचलेले आहेच. ही एक अतिप्राचीन संस्कृती होती. त्यांच्या अंकपद्धतीचा उगम जवळजवळ ५००० वर्षांपूर्वीचा आहे. त्यांच्या अंकपद्धतीत ६० हा मूलांक होता आणि स्थानीय किंमत ही संकल्पना पण त्यांनी वापरली होती. चिन्हे मुख्यत्वे दोनच होती. पाचरीसारखा दिसणारा खाली टोक असलेला त्रिकोण आणि साधारण तशीच पण डावीकडे टोक असलेली आकृती. एखाद्या फळीवर ओली माती पसरून त्यावर ह्या खुणांचे छाप उमटवले जात व नंतर ती माती वाळवली जाई. १० पेक्षा लहान संख्यांसाठी पाचरीची तितकी चिन्हे काढत. १० साठी डावीकडे टोक असलेली आकृती वापरली जात असे. अर्थातच २०, ३०, ४० इत्यादींसाठी ही आकृती तितक्या वेळा काढत. ६० हा मूलांक असल्याने त्यासाठी पण पाचर हेच चिन्ह वापरले जाई पण ते ’एकं’ स्थानाच्या पुढे. म्हणजे आपल्या दशम स्थानाचा १ म्हणजे जसे १० तशी एकं स्थानाच्या पुढच्या स्थानावरील एक पाचर म्हणजे ६० हा नियम होता. दोन ’स्थाने’ वेगळी दर्शविण्यासाठी त्यामध्ये थोडे अंतर ठेवत असत. पुढील तक्त्यावरून ह्या गोष्टी स्पष्ट होतील.
पुरातन कालातील अंकपद्धतीपैकी आणखी एक पद्धती म्हणजे चीनमध्ये वापरली जाणारी पद्धती. त्यात मुख्यत्वे उभ्या आणि आडव्या रेघा वापरून चिन्हे बनवलेली होती. त्यामुळे ह्या रेघांना काऊंटिंग रॉड्स असे म्हणत. ही चिन्हे ० ते ९ ह्या अंकांसाठी होती आणि १०, १००, १०००, १०००० इत्यादींसाठी वेगळी चिन्हे ठरवली होती. ह्या पद्धतीत संख्येत फेरफार करणे सहज शक्य होते त्यामुळे चिनी लोक आर्थिक व्यवहारासाठी वेगळी अंकचिन्हे वापरत असत.
अलीकडच्या काळात आणखी काही पद्धती अस्तित्वात आल्या. त्यापैकी एक म्हणजे द्विमान मद्धती. नावावरूनच लक्षात येईल की ह्यात मूलांक २ आहे. वापरली जाणारी चिन्हे पण अर्थातच ० आणि १ अशी आहेत. ह्या पद्धतीत आपल्याला अगदी लहानशी, उदा. २७ ही संख्या ११०११ अशी लिहावी लागेल. इथे स्थानिक किंमत १०च्या नव्हे तर २ च्या घातामध्ये (०,२,४,८,१६,३२) अशी असते. ही पद्धती आपल्याला नेहमीच्या व्यवहारात वापरणे अगदीच गैरसोयीचे आहे पण संगणकाला मात्र हीच पद्धती उपयुक्त ठरते. ८ हा मूलांक आणि १६ हा मूलांक असलेल्या अनुक्रमे अष्टमान आणि षोडशमान अशा पद्धती पण अस्तित्वात आहेत. षोडशमान पद्धतीचा मूलांक १६ असतो आणि त्यात ० ते ९ ह्या अंकांनंतर पुढील अंक इंग्रजी A,B,C,D,E,F ह्यांनी दर्शविले जातात. अष्टमान पद्धतीत अर्थातच ० ते ७ ही आठ चिन्हे असतात. ८ व १६ हे २ चे घात (अनुक्रमे २**३ आणि २**४) असल्याने द्विमान पद्धती आणि अष्टमान व षोडशमान पद्धतींशी थेट संबंध प्रस्थापित करता येतो. त्यामुळे ह्या पद्धती संगणकाशी संबंधित काही कामांसाठी वापरल्या जातात. दैनंदिन व्यवहारात मात्र ह्या अजिबात उपयोगी नाहीत.
सरतेशेवटी सध्या वापरात असलेल्या दशमान पद्धतीबद्दल थोडी अधिक माहिती पाहू. ह्या पद्धतीचा उगम भारतात साधारण इसवीसन १०० ते ५०० मध्ये झाला. अंकांसाठी वापरली जाणारी चिन्हे सुरुवातीला ब्राह्मी लिपीतील होती. चिन्हे ब्राह्मी असली तरी अंकपद्धती ब्राह्मी नव्हती. ब्राह्मी अंकपद्धतीत मूलांक आणि स्थानीय किंमत ह्या संकल्पना नव्हत्या. त्या भारतीयांनी दिल्या. आर्यभट्टाने एक सूत्र सांगितले आहे "स्थानं स्थानं दशगुणं।" म्हणजे प्रत्येक स्थान हे पूर्वीच्या स्थानाच्या दहापट असते. शून्याची संकल्पना देखील भारतीयांनी दिली. शून्य आणि स्थानीय किंमत ह्या दोन संकल्पनांमुळे ही पद्धती वापरण्यास फारच सोयीची झाली. कालांतराने चिन्हांमध्ये थोडा बदल झाला. ही चिन्हे आणि अंकपद्धती भारतातून पुढे पर्शियामध्ये गेली. तिथून अरबांपर्यंत पोहोचली. अरबांनी त्या चिन्हांमध्ये काही बदल केले. त्यानंतर अस्तित्वात आलेली आणि आज जवळजवळ जगभर वापरली जाणारी चिन्हे म्हणजे 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 ही भारतातून अरबांकडे आणि अरबांकडून युरोपात गेली. त्यामुळे त्यांना Arabic Numerals किंवा Hindu Arabic Numerals असे म्हणतात.
ह्या सर्वावरून एक गोष्ट लक्षात येईल की पूर्वीच्या अंकपद्धतींपैकी एक मायन पद्धती सोडली तर सर्वांत बऱ्याच त्रुटी होत्या. त्या वापरायला सोयीस्कर नव्हत्या, खूप मोठ्या संख्या त्यात लिहिणे जिकिरीचे होते. मायन पद्धतीतही २० हा मूलांक मानल्यावर २० चिन्हे ठरवणे हे अधिक तर्कसंगत झाले असते. चीनमध्येही दशमान पद्धत होती पण त्यात सुसूत्रता नव्हती. मोठ्या संख्या लिहिण्यासाठी वेगळी चिन्हे होती. आताची दशमान पद्धती मात्र तर्काधिष्ठित, सुटसुटीत तसेच लहान/मोठ्या, सर्वच संख्या लिहिण्यास सोयीस्कर आहे. शिवाय त्यात आकडेमोड करणेही फार कठीण नाही. त्यामुळे इतक्या अंकपद्धती पूर्वी होत्या पण त्या काही दूरवर पसरल्या नाहीत आणि जास्त काळ टिकल्याही नाहीत. दशमान पद्धती मात्र जगभर पसरली आणि अजूनही टिकून आहे. त्यामुळेच अंकपद्धतींच्या पंगतीत दशमानाला मानाचे पान मिळाले आहे!
-------------------------
टीपा:
१. लेखातील माहिती व चित्रे आंतरजालाच्या आधारे.
२. जालावर इजिप्शियन चिन्हांसंबंधी माहिती एकापेक्षा जास्त ठिकाणी मिळते. सगळीकडे चिन्हांचे वर्णन सारखेच असले तरी काही चिन्हांच्या चित्रांमध्ये थोडाफार फरक आढळतो.
महान भारतीय गणितज्ञ श्रीनिवास रामानुजन ह्याची १२५ जयंती ह्यावर्षी म्हणजे
२०१२ मध्ये आहे. त्यामुळे भारतात हे वर्ष गणितवर्ष म्हणून जाहीर केले गेले
आहे. त्या निमित्ताने केलेले हे थोडेसे लिखाण.