संदर्भ - सायमन सिंग यांच्या The Big Bang: The Origin of Universe या पुस्तकावरून अनुवादित.

प्राचीन खगोलशास्त्राची सुरूवात ग्रीक प्राकृतिक तत्त्ववेत्त्यांनी (Natural Philosophers) सूर्य, चंद्र, ग्रह-तारे यांसंबंधी केलेल्या निरीक्षणांपासून झाली. त्यांनी त्या निरीक्षणांवरून आणि गणिताचा उपयोग करून पृथ्वीचा परीघ, सूर्य आणि चंद्राचे परीघ, आणि त्यांची पृथ्वीपासून अंतरे कशी मोजली त्याची ओळख आपण या लेखात करून घेऊ.

चंद्र गोलाकार दिसतो आणि चंद्रग्रहणात चंद्रावर पडणारी पृथ्वीची सावली वर्तुळाकार असते यावरून सूर्य, चंद्र, पृथ्वी आणि ग्रह हे गोलाकार असावेत असा निष्कर्ष त्यांनी काढला. अर्थात, गोलाकारामुळे आजही मुलांना भेडसावणारा प्रश्न उभा राहतो तो असा की आपल्या विरुद्ध दिशेला (भारतात असू तर अमेरिकेतले किंवा उलट) राहणारे लोक खाली कसे पडत नाहीत? यावर ग्रीकांचे उत्तर असे की पृथ्वी ही विश्वाचे केंद्र आहे, त्यामुळे विश्वाचे केंद्र हे पृथ्वीच्या केंद्राशी एकरूप आहे. त्यामुळे विश्वातली प्रत्येक वस्तू पृथ्वीच्या केंद्राकडे आकर्षित होते. त्यामुळे विरुद्ध दिशेला राहणारे लोकही खाली पडत नाहीत.

त्यापुढची सर्वात महत्त्वाची उपलब्धी (achievement) म्हणजे इराटोस्थेनिसने पृथ्वीचा मोजलेला परीघ. ग्रीष्म संपाताच्या दिवशी साईन (Cyene) या कर्कवृत्तावर असणाऱ्या गावातल्या विहिरीच्या बरोबर वर सूर्य येतो या निरीक्षणाचा वापर करून पृथ्वीचा परीघ ३९,२५० किमी इतका भरतो असे त्याने दाखवून दिले. याबद्दल सविस्तर माहितीसाठी उपक्रम संकेतस्थळावरील दिवाळी २००८ ह्या अंकातील 'इराटोस्थेनिस आणि पृथ्वीचा परीघ' हा लेख पाहा. त्याच्या मोजणीतील त्रुटी २% होती की १५% हा मुद्दा गौण आहे कारण इराटोस्थेनिसच्या आधी पृथ्वीचा परीघ ४००० किमी आहे की ४,०००,००० किमी आहे याविषयी कोणालाही अंदाज नव्हता. त्यामुळे तो सुमारे ४०,००० किमी आहे हे सांगणे ही खरोखर मोठीच उपलब्धी होती.

एकदा पृथ्वीचा परीघ माहिती झाल्यावर चंद्राचा आकार काढणे सोपे होते, कारण त्यासाठी आवश्यक असणारे गणित आधीच्या प्राकृतिक तत्त्ववेत्त्यांनी आधीच मांडून ठेवले होते. ते फक्त पृथ्वीच्या परिघाची किंमत माहिती नसल्याने अपूर्ण राहिले होते.

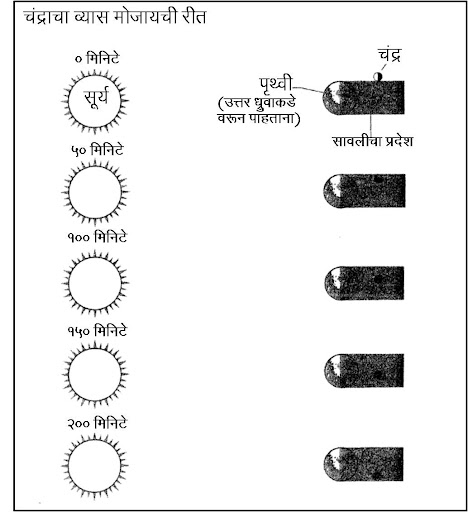
आकृती क्र. १: चंद्राचा व्यास मोजायची रीत

आकृती क्र. १ मध्ये चंद्राचा पृथ्वीच्या सावलीतून होणारा प्रवास क्रमाक्रमाने दाखवला आहे. पृथ्वी आणि चंद्र हे सूर्यापासून बरेच लांब आणि एकमेकांच्या जवळ असल्याने पृथ्वीची सावली बऱ्याच अंशी पृथ्वीच्या आकाराइतकीच आहे. ज्या ग्रहणात चंद्र पृथ्वीच्या सावलीच्या मध्यावरून प्रवास करतो त्यावेळी पृथ्वीच्या सावलीला स्पर्श केल्यापासून चंद्र संपूर्ण झाकला जाईपर्यंत ५० मिनिटे लागतात. म्हणजेच ५० मिनिटे हा काळ चंद्राच्या आकारमानाची कल्पना देणारा आहे. पृथ्वीच्या सावलीच्या एका टोकापासून दुसऱ्या टोकाला जायला चंद्राला २०० मिनिटे लागतात. म्हणजे २०० मिनिटे हा काळ पृथ्वीच्या आकारमानाशी सुसंगत आहे. याचा अर्थ असा की चंद्राचा व्यास पृथ्वीच्या व्यासाच्या एक चतुर्थांश आहे. आता इराटोस्थेनिसने पृथ्वीचा व्यास साधारण १२,७०० किमी असल्याचे दाखवून दिले होते त्यामुळे चंद्राचा व्यास अंदाजे ३२०० किमी. इतका भरतो.

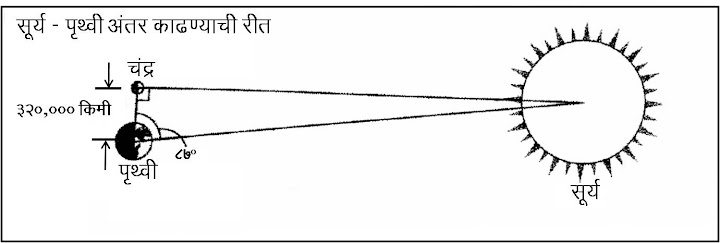
आकृती क्र. २: चंद्र - पृथ्वी अंतर काढण्याची रीत

आता चंद्राच्या व्यासावरून पृथ्वी आणि चंद्रामधले अंतर काढणे इराटोस्थेनिसला सोपे गेले. एक मार्ग म्हणजे पौर्णिमेच्या चंद्राकडे बघताना एक डोळा बंद करायचा आणि असे केल्यास तुमच्या लक्षात येईल की तुम्ही चंद्र बोटाच्या एका पेराने झाकू शकता. आकृती क्र. २ मध्ये दाखवल्याप्रमाणे तुमच्या बोटाच्या नखाचा तुमच्या डोळ्याशी एक त्रिकोण होतो. तशाच प्रकारचा पण आकाराने प्रचंड मोठा आणि समरूप (बाजूंचे प्रमाण तेच असणारा) त्रिकोण तुमचा डोळा आणि चंद्राच्या व्यासाची टोके यांमध्ये होतो. तुमच्या नखाची उंची आणि हाताची लांबी यांचे गुणोत्तर साधारण १ : १०० असे असते. समरूप त्रिकोणांमुळे चंद्राचा व्यास आणि चंद्राचे पृथ्वीपासूनचे अंतर यांचेही गुणोत्तर तितकेच असले पाहिजे. म्हणजेच पृथ्वीपासून चंद्राचे अंतर चंद्राच्या व्यासाच्या १०० पट असले पाहिजे. अर्थात चंद्र - पृथ्वीमधील अंतर ३,२०,००० किमी. झाले.

आकृती क्र. ३: सूर्य - पृथ्वी अंतर काढण्याची रीत

यापुढे ऍनाक्सागोरसचे गृहीतक आणि त्यावर आधारित ऍरिस्टार्कसचा तर्कशुद्ध युक्तिवाद यामुळे सूर्य - पृथ्वी यामधील अंतर आणि सूर्याचा व्यास काढणे शक्य झाले. ऍनाक्सागोरसने असे गृहीतक मांडले की सूर्य हा उष्ण पाषाण आहे तर चंद्र हा थंड पाषाण आहे. चंद्राला स्वतःचा प्रकाश नाही आणि तो सूर्याचा प्रकाश परावर्तित करतो. इसवी सन पूर्व तिसऱ्या शतकात ऍरिस्टार्कसने या गृहीतकाचा वापर करून सूर्य - पृथ्वीमधले अंतर काढले. चंद्र हा सूर्याचा प्रकाश परावर्तित करत असेल तर अष्टमीच्या दिवशी (हाफ मून) सूर्य, चंद्र आणि पृथ्वी आकृती क्र. ३ मध्ये दाखवल्याप्रमाणे एकमेकांशी काटकोनात असले पाहिजेत. ऍरिस्टार्कसने पृथ्वीला सूर्य आणि चंद्राशी जोडणाऱ्या रेषांमधला कोन मोजला आणि त्रिकोणमितीचा वापर करून सूर्य - पृथ्वी अंतराचे चंद्र - पृथ्वी अंतराशी असलेले प्रमाण काढले. त्याने हा कोन ८७° मोजला आणि त्यावरून सूर्य - पृथ्वी अंतर चंद्र - पृथ्वी अंतराच्या २० पट आहे असा निष्कर्ष काढला. आपल्या आधीच्या आकडेमोडीने चंद्र - पृथ्वी अंतर आपल्याला माहिती आहेच त्यामुळे सूर्य - पृथ्वी अंतरही मिळते. प्रत्यक्षात हा कोन ८९. ८५° इतका भरतो आणि सूर्य - पृथ्वी हे अंतर चंद्र पृथ्वी अंतराच्या ४०० पट भरते. त्यामुळे ऍरिस्टार्कसला हा कोन अचूक मोजता आला नाही हे खरे. तरीपण अचूकतेचा मुद्दा तितका महत्त्वाचा नाही. महत्त्वाचा मुद्दा हा आहे की ग्रीक लोकांनी सूर्य - पृथ्वी अंतर मोजण्याची योग्य पद्धती शोधून काढली ज्यामध्ये अचूक कोन मोजता आला तर सूर्य - पृथ्वी अंतर अचूक मिळू शकेल.

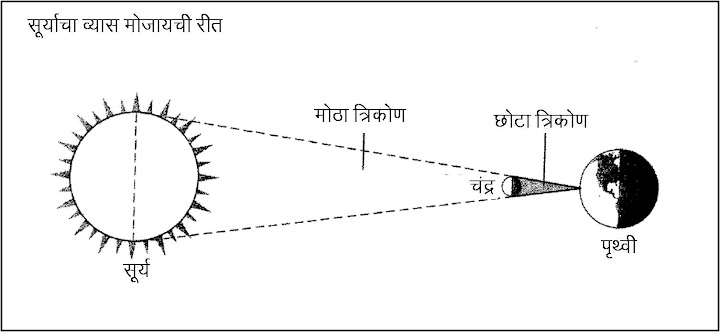
आकृती क्र. ४: सूर्याचा व्यास मोजायची रीत

शेवटचे म्हणजे सूर्याचा आकार मोजणे. हे त्यामानाने सोपे होते, कारण पृथ्वीवरून दिसणारी सूर्य आणि चंद्र यांची बिंबे सारख्याच आकाराची आहेत आणि खग्रास सूर्यग्रहणाच्या वेळेस चंद्र हा सूर्यबिंबास पूर्णपणे झाकतो. त्यामुळे, सूर्याचा व्यास आणि सूर्याचे पृथीपासून अंतर यांचे गुणोत्तर हे चंद्राचा व्यास आणि चंद्राचे पृथ्वीपासूनचे अंतर यांच्या गुणोत्तराइतकेच (जे साधारण १ : १०० आहे) असले पाहिजे. आकृती क्र. ४ मध्ये दाखवल्याप्रमाणे सूर्याचा व्यास काढता येतो. ही पद्धत आकृती क्र. ३ मध्ये दाखवल्यासारखीच आहे. फक्त यात बोटाच्या नखाची जागा, आकार आणि अंतर माहिती असलेली वस्तू म्हणून, चंद्राने घेतली आहे.

(चित्रे आंतरजालावरून साभार.)

इराटोस्थेनिस आणि ऍरिस्टार्कस यांच्या या आश्चर्यकारक उपलब्धी त्या काळातील प्राचीन ग्रीसमध्ये होणाऱ्या शास्त्रशुद्ध विचारांची प्रगती दर्शवणाऱ्या आहेत. कारण त्यांचे विश्वाचे मोजमाप तर्क, गणित, निरीक्षण आणि मापन या गोष्टींवर आधारलेले होते.
थोडक्यात, ग्रीक लोकांनी हे दाखवून दिले की सूर्याचा व्यास काढणे हे सूर्य - पृथ्वी अंतर माहिती असण्यावर अवलंबून आहे, सूर्य - पृथ्वी अंतर काढण्याकरता चंद्र - पृथ्वी अंतर माहिती असायला हवे आणि त्यासाठी चंद्राचा व्यास आधी कळायला हवा. चंद्राचा व्यास समजायचा तर पृथ्वीचा व्यास माहिती हवा आणि तीच इराटोस्थेनिसची अत्यंत महत्त्वाची उपलब्धी. सूर्य, चंद्र आणि पृथ्वी यांमधली अंतरे आणि त्यांचे आकार मोजण्याच्या या पायऱ्या चढून जाणे हे कर्कवृत्तावरील खोल विहीर, चंद्रग्रहणातील पृथ्वीची चंद्रावरील छाया, अष्टमीच्या दिवशी सूर्य, चंद्र आणि पृथ्वी काटकोनात असतात ही गोष्ट, आणि सूर्यग्रहणात चंद्र सूर्यबिंबावर अचूक बसतो हे निरीक्षण, या गोष्टींचा वापर केल्याने शक्य झाले. यामध्ये चंद्रप्रकाश हा परावर्तित सूर्यप्रकाश आहे अशासारख्या गृहीतकांची भर घातली की वैज्ञानिक तर्कशास्त्राचे (scientific logic) एक स्वतंत्र स्थापत्यशास्त्र (architecture) उभे राहते. या स्थापत्यशास्त्राला स्वतःचे असे एक सौंदर्य आहे, ज्यामध्ये निरनिराळे युक्तिवाद एकमेकांशी सुसंगत होतात, निरनिराळी मोजमापे एकमेकांना पूरक ठरतात आणि त्या स्थापत्यरचनेला (edifice) शक्ती देणाऱ्या निरनिराळ्या सिद्धातांची भर त्यात घातली जाते.

ऍरिस्टार्कसने सूर्य - पृथ्वीमधले अंतर मोजले ही उपलब्धी दुय्यम ठरावी अशी एक गोष्ट त्याने पुढे केली. त्याने सूर्य विश्वाच्या केंद्रस्थानी असून पृथ्वीसह इतर ग्रह त्याच्याभोवती वर्तुळाकार कक्षेत फिरतात असा सिद्धांत मांडला. त्या सिद्धांताबद्दलची माहिती, त्यावर त्याकाळच्या लोकांनी घेतलेले आक्षेप आणि त्यांचे निराकरण वगैरे गोष्टी इतरत्र विस्ताराने लिहीन.